在数学的世界里,方程是连接已知与未知的桥梁,而一元二次方程无疑是这座桥梁上的一颗璀璨明珠,作为博客站长,今天我将带领大家深入探讨一元二次方程的求根公式法,这一解决此类方程最基本且最常用的方法。
求根公式法简介
求根公式法,又称公式法,是解一元二次方程ax^2 + bx + c = 0(其中a ≠ 0)的一种系统化、程序化的方法,通过计算判别式Δ = b^2 - 4ac的值,我们可以直接利用求根公式得出方程的解,求根公式有两个解,分别为x1和x2,计算公式如下:
x1 = (-b + √(b^2 - 4ac)) / (2a)
x2 = (-b - √(b^2 - 4ac)) / (2a)
√表示平方根,这个公式在数学上被广泛应用,是求解一元二次方程不可或缺的工具。
求根公式法的步骤
使用求根公式法解一元二次方程,通常遵循以下步骤:
1、将方程化为一般形式:我们需要将一元二次方程化为ax^2 + bx + c = 0的一般形式,并确定a、b、c的值。
2、计算判别式Δ:判别式Δ = b^2 - 4ac是判断方程根的情况的关键,根据Δ的值,我们可以确定方程的根是实数根还是虚数根,以及根的数量。
- 当Δ > 0时,方程有两个不相等的实数根。
- 当Δ = 0时,方程有两个相等的实数根。
- 当Δ < 0时,方程无实数根,但有两个共轭的虚数根。
3、代入求根公式计算根:当Δ ≥ 0时,我们可以将a、b、c及Δ的值代入求根公式,计算出方程的解x1和x2。
求根公式法的应用实例
为了更好地理解求根公式法的应用,我们来看几个具体的例子:
例1:解方程2x^2 - 7x = -3。
将方程化为一般形式:2x^2 - 7x + 3 = 0。
计算判别式Δ:Δ = (-7)^2 - 4 * 2 * 3 = 49 - 24 = 25。
由于Δ > 0,方程有两个不相等的实数根。
代入求根公式计算根:
x1 = (-(-7) + √(25)) / (2 * 2) = (7 + 5) / 4 = 3
x2 = (-(-7) - √(25)) / (2 * 2) = (7 - 5) / 4 = 1/2
例2:解方程8x^2 + 10x = 3。
将方程化为一般形式:8x^2 + 10x - 3 = 0。
计算判别式Δ:Δ = 10^2 - 4 * 8 * (-3) = 100 + 96 = 196。
由于Δ > 0,方程有两个不相等的实数根。
代入求根公式计算根:
x1 = (-10 + √(196)) / (2 * 8) = (-10 + 14) / 16 = 1/4
x2 = (-10 - √(196)) / (2 * 8) = (-10 - 14) / 16 = -3/2
求根公式法的意义与局限
求根公式法的意义在于它提供了一种系统化、程序化的解决一元二次方程的方法,避免了繁琐的配方过程,直接得出方程的解,这种方法不仅适用于简单的一元二次方程,也适用于复杂的一元二次方程,只要能够确定a、b、c的值,就可以通过计算判别式Δ和代入求根公式得出解。
求根公式法也有其局限性,它只适用于一元二次方程,对于一元三次方程、一元四次方程等高阶方程,虽然也存在相应的求根公式,但求解过程更加复杂,且不存在类似于求根公式那样的通用解法,当判别式Δ < 0时,方程无实数根,此时求根公式得出的解为虚数根,这在某些实际问题中可能无实际意义。
求根公式法是解一元二次方程最基本且最常用的方法,它提供了一种系统化、程序化的解决思路,使我们能够轻松应对各种形式的一元二次方程,通过计算判别式Δ和代入求根公式,我们可以直接得出方程的解,为数学问题的解决提供了有力的工具,我们也需要认识到求根公式法的局限性,并在实际应用中灵活运用各种方法,以求解更复杂、更实际的数学问题。
作为博客站长,我希望通过这篇文章,能够帮助大家更好地理解求根公式法,掌握其应用技巧,并在数学学习的道路上越走越远,让我们携手共进,探索数学的奥秘,享受数学带来的乐趣吧!
转载请注明来自广西蓝创新能源汽车设备有限公司,本文标题:《求根公式法,一元二次方程的快速解锁秘籍》







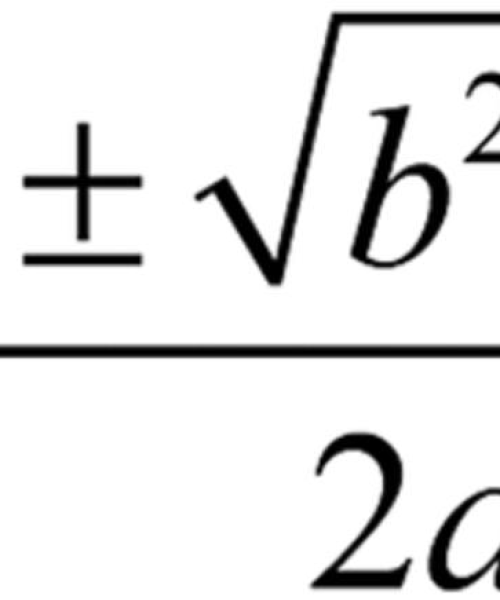



 桂ICP备17012074号-1
桂ICP备17012074号-1
还没有评论,来说两句吧...